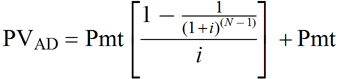
This is illustrated graphically in the section that follows, “Visual Comparison of Cash Flows.” It can also be clearly seen in the discount and accumulation schedules constructed in the “Excel” section. They can arise in loans, retirement plans, leases, insurance settlements, tax-related calculations, and so forth. Sometimes, one may be curious to learn how much a recurring stream of payments will grow to after a number of periods. This future value of an annuity due formula is an investigative tool that is used to estimate the total value of cash payments made at the beginning of a pay period.
This problem calculates the difference between the present value (PV) of an ordinary annuity and an annuity due. The timing difference in the payments is illustrated in an Excel schedule.
Checking out the preceding figure, you see that the factor is 6.8017. Just like with the future value of an annuity due, you have to consider an additional factor of 1 plus the interest rate.
It is important to note that, in this formula, the interest rate must remain the same through the series, and payment amounts must be equally distributed. If the payments differ during the series, or if the interest rates will change over time, there isn’t a formula to calculate the future value of that particular annuity due. The formula for the present value of an annuity due, sometimes referred to as an immediate annuity, is used to calculate a series of periodic payments, or cash flows, that start immediately.
PVIFA is also used in the formula to calculate the present value of an annuity. Once you have the PVIFA factor value, you can multiply it by the periodic payment amount to find the current present value of the annuity. The present value of an annuity due (PVAD) is calculating the value at the end of the number of periods given, using the current value of money. Another way to think of it is how much an annuity due would be worth when payments are complete in the future, brought to the present. shows that the first cash flow is not discounted and that the discounted cash flows start at period 2.
What Is the Present Value of an Annuity?
Although the graphic provides a useful explanatory tool, it is a bit cumbersome to implement. The same conclusion can be reached by reference to a future value of an annuity due table. Multiplying the $5,000 annual payment by this factor yields $33,578 ($5,000 X 6.71561). An annuity due is an annuity where the payments are made at the beginning of each time period; for an ordinary annuity, payments are made at the end of the time period.
Create a printable compound interest table for the present value of an ordinary annuity or present value of an annuity due for payments of $1. Future value of an annuity due is used to predict the future value of a series of payments where the payment is made immediately at the beginning of the payment period. The payment at the beginning of the period is the main difference between an annuity due and an ordinary annuity. If annuity payments are due at the beginning of the period, the payments are referred to as an annuity due.
Time Value of Money
- It is possible to calculate the future value of an annuity due by hand.
- To do this, you could make a chart to list the amounts of the payments being made.
Higher interest rates result in lower net present value calculations. This is because the value of $1 today is diminished if high returns are anticipated in the future.
Present Value Annuity Due Tables
It is possible to calculate the future value of an annuity due by hand. To do this, you could make a chart to list the amounts of the payments being made. You would identify the payment periods and the set interest rate through the time limit you have set. The future value of an annuity due formula is used to predict the end result of a series of payments made over time, including the income that is made from their associated interest rates. The term “value” refers to the potential cash flow that a series of payments can achieve.
To calculate the present value interest factor of an annuity due, take the calculation of the present value interest factor and multiply it by (1+r), with the variable being the discount rate. The present value interest factor of an annuity is useful when determining whether to take a lump-sum payment now or accept an annuity payment in future periods. Using estimated rates of return, you can compare the value of the annuity payments to the lump sum.
The present value interest factor may only be calculated if the annuity payments are for a predetermined amount spanning a predetermined range of time. Note also that the above formula implies that both the PV and the FVof an annuity due will be greater than their comparable ordinary annuity values.
The Excel FV function is a financial function that returns the future value of an investment. You can use the FV function to get the future value of an investment assuming periodic, constant payments with a constant interest rate. The present value (PV) of an annuity due is the value today of a series of payments in the future. It uses a payment amount, number of payments, and rate of return to calculate the value of the payments in today’s dollars.
So you multiply 1.06 times 6.8017 to get the present value of an annuity due, which is 7.2098. Just like the future value of annuities due, the present value of an annuity due calculates annuities taking place sooner — that is, at the beginning instead of end of the period. You can use the future value of an annuity due calculator below to quickly work out the potential cash flow of monthly payments by entering the required numbers. The initial payment earns interest at the periodic rate (r) over a number of payment periods (n).
The discount rate used in the present value interest factor calculation approximates the expected rate of return for future periods. It is adjusted for risk based on the duration of the annuity payments and the investment vehicle utilized.
So by looking at the future value, we are calculating this potential at a future date in time. Calculate the present value interest factor of an annuity (PVIFA) and create a table of PVIFA values.