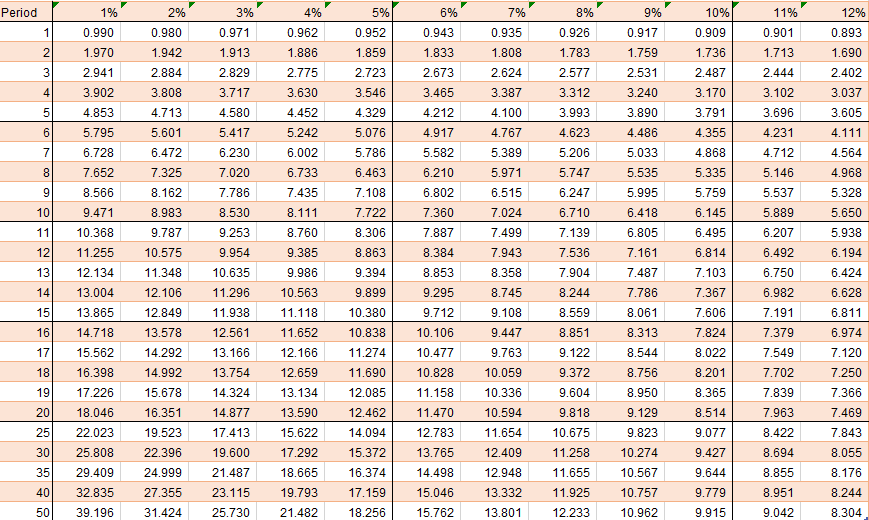
So it’s just the notion of you’re definitely going to get $100 today in your hand, or you’re definitely going to get $110 one year from now. What if there were a way to say, well what is $110, a guaranteed $110, in the future? What if there were a way to say, how much is that worth today? Let’s say that you could put money in the bank. But let’s say you could put it in the safest bank in the world.
If we have a certain amount of money and we want to figure out today’s value, what could we do? Well, to go from here to here, what did we do? We essentially took $100 and we multiplied by- what did we multiply by– 1 plus 5%. So to go the other way, to say how much money, if I were to grow it by 5%, would end up being $110?
The differences in future value from investing at these different rates of return are small for short compounding periods (such as 1 year) but become larger as the compounding period is extended. As the length of the holding period is extended, small differences in discount rates can lead to large differences in future value. In a study of returns on stocks and bonds between 1926 and 1997, Ibbotson and Sinquefield found that stocks on the average made 12.4%, treasury bonds made 5.2%, and treasury bills made 3.6%. Assuming that these returns continue into the future, Table 3.1 provides the future values of $ 100 invested in each category at the end of a number of holding periods – 1 year, 5 years, 10 years, 20 years, 30 years, and 40 years. We’ll now learn about what is arguably the most useful concept in finance, and that’s called the present value.
So assuming I don’t have to spend the money today, this is a better situation to be in, right? If I take the money today, and risk-free invest it at 5%, I’m going to end up with $105 in a year. Instead, if you just tell me, Sal, just give me the money in a year– give me $110– you’re going to end up with more money in a year, right?
So to some degree when you took this $100 and you said well if I lend it to the government, or if I lend it to a risk-free bank at 5%, in a year they’ll give me $105. This $105 is a way of saying what is the one-year value of $100 today? So what if we wanted to go in the other direction?
The present value interest factor of an annuity (PVIFA) is useful when deciding whether to take a lump-sum payment now or accept an annuity payment in future periods. Using estimated rates of return, you can compare the value of the annuity payments to the lump sum. Present value calculations, and similarly future value calculations, are used to value loans, mortgages, annuities, sinking funds, perpetuities, bonds, and more.
Treasury, which essentially is you’re lending money to the U.S. government, that it’s risk-free. So let’s say today I could give you $100 and that you could invest it at 5% risk-free. And then in a year from now, how much would that be worth, in a year? You’re like, OK, instead of taking the money from Sal a year from now and getting $110, if I were to take $100 today and put it in something risk-free, in a year I would have $105.
Present Value Factor Calculator
And if you know the present value, then it’s very easy to understand the net present value and the discounted cash flow and the internal rate of return. And we’ll eventually learn all of those things. Or, and it’s up to you, in one year I will pay you– I don’t know– let’s say in a year I agree to pay you $110.
The present value interest factor (PVIF) is a formula used to estimate the current worth of a sum of money that is to be received at some future date. PVIFs are often presented in the form of a table with values for different time periods and interest rate combinations. The concepts of present value and present value factors play an important role in investment valuation and capital budgeting. Say, the present value of future cash inflows exceeds the present cash outflow of $1000, then the machinery is worth investing, else it would serve better for Company S to invest the money in other more profitable avenues. The annuities considered thus far in this chapter are end-of-the-period cash flows.
These calculations are used to make comparisons between cash flows that don’t occur at simultaneous times, since time dates must be consistent in order to make comparisons between values. When deciding between projects in which to invest, the choice can be made by comparing respective present values of such projects by means of discounting the expected income streams at the corresponding project interest rate, or rate of return. The project with the highest present value, i.e. that is most valuable today, should be chosen. Present value means today’s value of the cash flow to be received at a future point of time and present value factor formula is a tool/formula to calculate a present value of future cash flow. The concept of present value is useful in making a decision by assessing the present value of future cash flow.
We’ll get the present value of $110 a year from now. So the present value of $110, let’s say in 2009. I don’t know what year you’re watching this video in.
- The process by which future cash flows are adjusted to reflect these factors is called discounting, and the magnitude of these factors is reflected in the discount rate.
- The discount rate incorporates all of the above mentioned factors.
- This formula is centered on the idea of assessing if an ongoing investment can be encashed and utilized better to enhance the final outcome as compared to an original outcome that can be had with the current investment.
Use of the Present Value Factor Formula
And that is actually the right way to think about it. And remember, and I keep saying it over and over again, everything I’m talking about, it’s critical that we’re talking about risk-free. Once you introduce risk, then we have to start introducing different interest rates and probabilities. But I want to just give the purest example right now. But we still don’t know what the present value was.
Annuity Derivation Vs. Perpetuity Derivation: What’s the Difference?
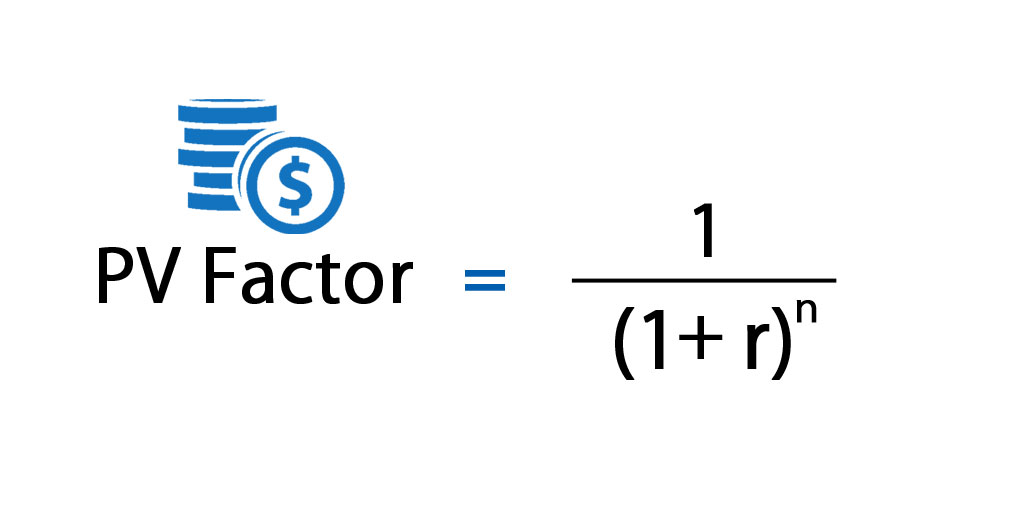
Let’s say you , although someone would debate, you put it in government treasuries. Which are considered risk-free, because the U.S. government, the Treasury, can always indirectly print more money. We’ll one day do a whole thing on the money supply. But at the end of the day, the U.S. government has the rights on the printing press, et cetera. But for those purposes, we assume that with the U.S.
And my question to you– and this is a fundamental question of finance, everything will build upon this– is which one would you prefer? I’m either going to pay you $100 today, and there’s no risk, even if I get hit by a truck or whatever. The U.S. government, if the earth exists, we will pay you $110 in one year.
Present Value Interest Factor
To compound the amount of money we invest, we multiply the amount we invest times 1 plus the yield. Then to discount money in the future to the present, we divided by 1 plus the discount rate– so this is a 5% discount rate– to get its present value. This tells us if someone’s willing to pay $110, assuming this 5%– remember this is a critical assumption. So if this comparison were– let me clear all of this, let me just scroll down– so let’s say that today, 1 year. So we figured out that $110 a year from now, its present value is equal to– so the present value of that $110– is equal to $104.76.
Hopefully people will be watching this in the next millennia. But the present value of $110 in 2009, assuming right now it’s 2008, a year from now, is equal to $110 divided by 1.05. And let’s take out this calculator, which is probably overkill for this problem. OK so I want to do 110 divided by 1.05 is equal to– let’s just round– so it equals $104.76. So the present value of $110 a year from now, if we assume that we could invest money risk-free at 5%, if we were to get it today — let me do it in a different color just to fight the monotony– the present value is equal to $104.76.
With a view to estimating what would be the current value of a certain sum to be received on a future date, we need two factors, namely, the time interval after which the sum is to be received and the rate of return for the same. These two factors can then be used to calculate the present value factors for any given sum to be received on any given future date. Present value impact factors are often used in analyzing annuities.
The process by which future cash flows are adjusted to reflect these factors is called discounting, and the magnitude of these factors is reflected in the discount rate. The discount rate incorporates all of the above mentioned factors. This formula is centered on the idea of assessing if an ongoing investment can be encashed and utilized better to enhance the final outcome as compared to an original outcome that can be had with the current investment.
Both the present and future values will be affected if the cash flows occur at the beginning of each period instead of the end. To illustrate this effect, consider an annuity of $ 100 at the end of each year for the next 4 years, with a discount rate of 10%.
Another way to kind of just talk about this is to get the present value of $110 a year from now, we discounted the value by a discount rate. Right here we grew the money by, you could say, our yield. Here we’re discounting the money, because we’re going backwards in time.