
Present Value – PV
This is because the money you have today can be invested in an interest-earning account and gain value over time. In other words, it’s better to have $10 today than $10 one year in the future because you can invest your $10 today and have more than $10 in a year. For NPV calculations, you need to know the interest rate of an investment account or opportunity with a similar level of risk to the investment you’re analyzing. This is called your “discount rate” and is expressed as a decimal, rather than a percent.
The Excel NPV function is a financial function that calculates the net present value (NPV) of an investment using a discount rate and a series of future cash flows. Project X requires an initial investment of $35,000 but is expected to generate revenues of $10,000, $27,000 and $19,000 for the first, second, and third years, respectively. Since the cash inflows are uneven, the NPV formula is broken out by individual cash flows.
An investor can decide which project to invest in by calculating each projects’ present value (using the same interest rate for each calculation) and then comparing them. The project with the smallest present value – the least initial outlay – will be chosen because it offers the same return as the other projects for the least amount of money.
Then we take the $1,800 and discount it two periods at 15% and we get $1,361.06. Now when we sum the present value of all those cash flows, we get minus $334.59, which tells us that the project destroys value. The decision rule is whether NPV is bigger than 0 or less than 0. We can construct the formula for NPV by following along very closely with what we did in the prior blog post discounting cash flows.
The discount rate is the investment rate of return that is applied to the present value calculation. In other words, the discount rate would be the forgone rate of return if an investor chose to accept an amount in the future versus the same amount today. The discount rate that is chosen for the present value calculation is highly subjective because it’s the expected rate of return you’d receive if you had invested today’s dollars for a period of time. Future cash flows are discounted at the discount rate, and the higher the discount rate, the lower the present value of the future cash flows. Determining the appropriate discount rate is the key to properly valuing future cash flows, whether they be earnings or obligations.
What is the present value formula?
Present value models are based on a fundamental tenet of economics stating that individuals defer consumption in order to reap future benefits. Therefore, the value of an investment today should be worth the present value of expected future benefits, defined as dividends or free cash flow.
To calculate NPV you need to estimate future cash flows for each period and determine the correct discount rate. Net present value(NPV) is a method used to determine the current value of all futurecash flowsgenerated by a project, including the initial capital investment. It is widely used incapital budgetingto establish which projects are likely to turn the greatest profit. The next formula presents this in a form that is easier to calculate. You could read (PV(1 + I)ⁿ) as, “the present value (PV) times (1 + I)ⁿ”, where l represents the interest rate and the superscript ⁿis the number of compounding periods.
PV Formula and Calculation
NPV is the gold standard but using it along with IRR makes for even better analysis and decision making. I will talk about IRR (internal rate of return) in a future blog post. The accuracy of any NPV calculation basically depends on the accuracy of the values you use for your discount rate and your future cash inflows.
Do You Include Working Capital in Net Present Value (NPV)?
In this case, the bank is the borrower of the funds and is responsible for crediting interest to the account holder. A compounding period is the length of time that must transpire before interest is credited, or added to the total. For example, interest that is compounded annually is credited once a year, and the compounding period is one year. Interest that is compounded quarterly is credited four times a year, and the compounding period is three months.
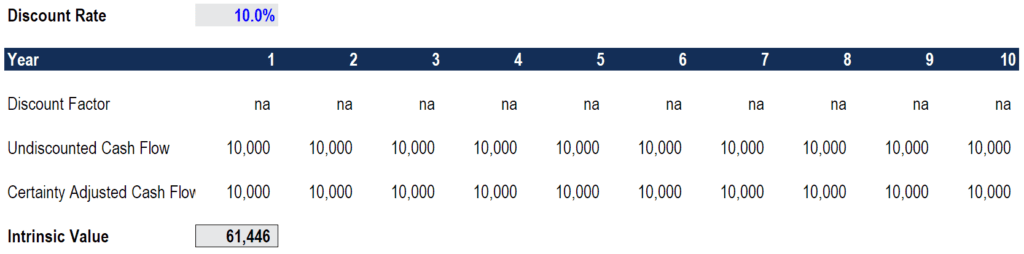
- NPV calculates the net present value (NPV) of an investment using a discount rate and a series of future cash flows.
- The discount rate is the rate for one period, assumed to be annual.
- NPV in Excel is a bit tricky, because of how the function is implemented.
Discount your cash inflows, them add them all together and subtract your initial investment. If the answer is a positive number, this indicates a good investment. If the answer is a negative number, the investment isn’t profitable.
Calculating Present and Future Value of Annuities
The required rate of return is used as thediscount ratefor future cash flows to account for thetime value of money. A dollar today is worth more than a dollar tomorrow because a dollar can be put to use earning a return. Therefore, when calculating the present value of future income, cash flows that will be earned in the future must be reduced to account for the delay. In general, a given amount of money is worth more now than it is in the future.
The NPV formula is a way of calculating the Net Present Value (NPV) of a series of cash flows based on a specified discount rate. The NPV formula can be very useful for financial analysis and financial modeling when determining the value of an investment (a company, a project, a cost-saving initiative, etc.). Present value (PV) is the current value of a future sum of money or stream of cash flows given a specified rate of return. Present value takes the future value and applies a discount rate or the interest rate that could be earned if invested. For example, money deposited into a savings account earns a certain interest rate and is therefore said to be compounding in value.
NPV calculates the net present value (NPV) of an investment using a discount rate and a series of future cash flows. The discount rate is the rate for one period, assumed to be annual. NPV in Excel is a bit tricky, because of how the function is implemented. Although NPV carries the idea of “net”, as in present value of future cash flows less initial cost, NPV is really just present value of uneven cash flows.
If offered a choice between $100 today or $100 in one year, and there is a positive real interest rate throughout the year, ceteris paribus, a rational person will choose $100 today. Time preference can be measured by auctioning off a risk free security—like a US Treasury bill. If a $100 note with a zero coupon, payable in one year, sells for $80 now, then $80 is the present value of the note that will be worth $100 a year from now. This is because money can be put in a bank account or any other (safe) investment that will return interest in the future.
Interest is the additional amount of money gained between the beginning and the end of a time period. Interest represents the time value of money, and can be thought of as rent that is required of a borrower in order to use money from a lender. For example, when an individual takes out a bank loan, the individual is charged interest. Alternatively, when an individual deposits money into a bank, the money earns interest.
Limitations of Using PV
We need to adjust the cash flows for the time value of money by discounting them to the present value. We take that $1,500 and discount it one period at 15% and we get $1,304.35.
What is Present Value example?
Present Value Formula PV = Present value, also known as present discounted value, is the value on a given date of a payment. r = the periodic rate of return, interest or inflation rate, also known as the discounting rate.
The NPV calculation involves discounting all cash flows to the present based on an assumed discount rate. When the discount rate is large, there are larger differences between PV and FV (present and future value) for each cash flow than when the discount rate is small. Thus, when discount rates are large, cash flows further in the future affect NPV less than when the rates are small. Conversely, a low discount rate means that NPV is affected more by the cash flows that occur further in the future.
Next, we’ll weight the value of our cash inflows for each time period we’re analyzing against the amount of money we’ll make from our alternate investment in the same period. This is called “discounting” the cash flows and is done using the simple formula P / (1 + i)t, where P is the amount of the cash flow, i is the discount rate, and t represents time. The Internal Rate of Return (IRR) is the discount rate that makes the net present value (NPV) of a project zero. In other words, it is the expected compound annual rate of return that will be earned on a project or investment. The project claims to return the initial outlay, as well as some surplus (for example, interest, or future cash flows).
A compounding period can be any length of time, but some common periods are annually, semiannually, quarterly, monthly, daily, and even continuously. To calculate NPV, write down the amount of your investment, the time period you want to analyze, the estimated cash flow for that time period, and the appropriate discount rate.